The question has been asked: How do we generalize special relativity? This seems easy to do in one spatial dimension. All we need is a suitable transformation group. Spacetime geometry is defined by a group of transformations.

It only takes solving one functional equation to create infinitely many generalizations of the Lorentz transformation. The problem is how to find the invariants of a given abstract group and interpret its geometric meaning physically. Let me illustrate the difficulty for you.

Let c=1.

Let and be a one-parameter family of functions.

Set:

Assume this transformation has the group property. Then:

Solve these functional equations by just writing down the answer:

and is the inverse function of f and g respectively.

There it is: A glorious nonlinear version of the Lorentz transformation group. 

You’ll notice immediately that if f(x)=x and g(x)=x, a=-1 and b=1, then we get the ordinary Lorentz transformation:

which is more typically written as:

where .

The problem with the proposed, nonlinear solution is that it violates the principle of relativity, i.e., the equivalence of all inertial frames of reference. The requirement of indistinguishable frames is a very powerful mathematical constraint! When the indistinguishability restrictions are applied to this group, one finds that the only admissible solutions are linear and that a=-b.

We must have a model of 2-dimensional gravity!

There’s one instructive generalization of the Lorentz transformation that works well as a difficult to believe counterexample. It’s just ordinary relativity in disguise. Take the Lorentz transformation and reset all the clocks in any nontrivial manner at every point in all frames of reference. The end result demonstrates that the transformation equations need not be linear. I’ll leave you to prove that as an exercise.

1. Let be a function of x. Prove that the set of all transformations of the form:

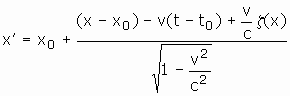
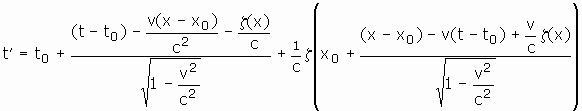
is a group.

2. Prove that this group is physically indistinguishable from the Lorentz group.

Do you have a question or comment?
Follow it up in our Discussion Forum.