What are the Logical Implications of an Absolute Frame of Reference?
In Physical Review D, Volume 8, Number 6, 15 September 1973, there is a curious paper titled, “Unaccelerated-Returning-Twin Paradox in Flat Space-Time.” ◊ In that paper, the twin paradox is considered for the simplest spacetime universe, i.e., the cylinder SxR. In their opening abstract, the authors, Carl H. Brans and Dennis Ronald, state, and I quote:
|
I do agree with most of their analysis. My conclusion about the outcome of the twin paradox for this universe is similar. ≈ Still, I find it strange that the startling implications of the global analysis of SxR haven’t been mentioned in a single university textbook on physics. There is no popular account of relativity that explains the result. I have brought up the elementary spacetime physics of SxR on the newsgroups sci.physics and sci.physics.relativity and have found that all the posters who responded, from informed Ph.Ds down to illiterate trolls, were in total denial of the physics and were absolutely incensed that the idea should even be debated.
What follows is a more careful exposition and a more complete set of results, which surpasses that paper that was published 30 years ago.
Einstein’s Religion
You all know that Albert Einstein was deeply religious in his pantheistic
veneration of the physics of nature. No scientist today should be
surprised to learn that Einstein was completely wrong about true religion.
This paper is about outrageously religious ideas in the philosophy of
physics.
Einstein’s greatest blunder in science was his stubborn, unrealistic faith in a deterministic universe. His belief in a mechanistic interpretation for all natural law is widely recognized as a direct denial of quantum physics and the Hebrew Bible. Einstein would express his faith by saying, “Gott wurfelt nicht!” (God does not play dice!) Of course God plays dice with light and matter. God not only plays dice with the universe, —He cheats. (I don’t mean to review the philosophical/religious underpinnings of quantum mechanics in this paper).
Einstein’s second greatest scientific blunder, which he never repudiated, was his fallacy of no absolute time order for all events in the universe and that we may not conceptualize time being divided into an absolute past, present and future.
“For us believing physicists, the distinction between past, present, and future is only an illusion, even if a stubborn one.” —Albert Einstein.
|
Einstein’s sophistry about time order being relative is clever and compelling but it’s inconsistent with Einstein’s favorite cosmological model. All of Einstein’s watchful, guarded reasoning in the famous train and embankment gedanken experiment derails itself in a spatially closed and bounded universe. I will demonstrate how an absolute time order follows from the laws of physics in Einstein’s universe. The argument is easy. Here are the key ideas:
If a law is a true law of physics, then it’s true everywhere, for all time. There is a universal speed law of light propagation. It’s impossible to prove global theorems about time order with an insufficient array of synchronized clocks. A consistent, global view of synchronization and spacetime, based on a universal speed law of light propagation, outranks all local, partial and limited views of the universe.
Implications
There are two ideas that are very prevalent in both
popular and professional expositions of the theory of general relativity.
1). The universe is spatially compact. 2). It is possible to fall into a
black hole. This paper will prove that both concepts can’t be true at
the same time.
A Global Theorem
Introduction
The best way to understand special relativity is to try to derive special
relativity on a circle. A true understanding of a spatially closed and
bounded universe obviously begins here.
Einstein’s special theory of relativity is based on
two postulates:
1. The laws of physics are the same for all observers
in all inertial frames of reference.
2. The speed of light in vacuum has the same constant
value c for all observers in all inertial frames of reference.
In the case where space S is just a circle, spacetime is incredibly easy to understand. Consider the impossibility of the second postulate in the spatially compact (i.e., spatially closed and bounded) universe SxR.
Assume that the postulates of special relativity apply to the greatest extent that they can.
Let two observers in relative motion pass each other at time t'=t=0. At that instant, let two photons be emitted in opposite directions. Let inertial observers a, b note the place and time of this event as (x,t) =(0,0); (x',t') =(0,0), respectively. To not distract from the physics, think of the relative velocity v of these observers as being relatively small. The photons will circumnavigate the universe and coincide at a unique event. The photons can’t arrive together at both a and b because these have moved some distance apart. Consequently—in this spatially compact universe—there is a uniquely distinguished frame of reference that can only be seen on the global scale.
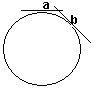
It’s obvious from the notion of measure that the distance around the universe is the same in both directions. The size of the universe may be relative for different observers but that doesn’t resolve the paradox. Nevertheless, if there were a way to understand this spacetime, it would only appear mathematically. It’s time to formulize our results quantitatively.
Starting from assumptions that even non-relativists should accept, the following equations express—in a very general and meaningful way—the coordinates of events of one inertial observer in terms of another:
 
|
We’ll start here. If you’re interested in the physical interpretation of this transformation and its presuppositions, please see my first derivation of special relativity. Click here.
If we had enough time in our universe to watch opposing photon bursts circumnavigate the universe, we could identify the uniquely distinguished rest frame. Let the unprimed coordinates refer to this absolute frame of reference.
I will use the following essential facts:
From elementary calculus we know that velocity transforms according to the following rule:
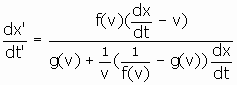
Let c be the speed of light in the rest frame 
.
Then x=ct and x=-ct implies that 
and 
respectively, where
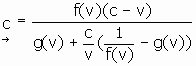
Let 
be the distance around the
universe as measured in 
.
Let (0, 
)
be the event in where two opposing photon bursts
return to their place of origin. This event (the great illumination)
according to the coordinates of the nearby moving frame
is (x',t') = (
, 
). This means that the distance in between the
two coordinate origins at the time of the great illumination is the
absolute value of .
Note this also. When the photons arrive at x'=,
the two bursts are still traveling in opposite directions. To a local
observer in the frame ,
the photons moving away from x'=0 have already been there and have
traveled the distance 
. The
photons headed toward x'=0 have only traveled the distance 
.
Considering the elapsed time and position of the photons for this event,
we see that
Subtract one equation from another and get
This is a constraint on the general form of our coordinate transformation:
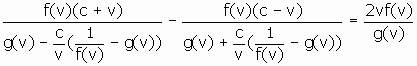
The identity implies that 
.
This simplifies things a bit giving us as the final form of the
transformation equations:
|
|
An earlier result now reads:
Therefore 
is the distance around the
universe in the absolute frame of reference. Therefore 
is the distance around the universe in our moving frame.
We have assumed that the postulates of special
relativity apply in the greatest extent possible. Consider now the two-way
speed of light in the moving frame .
From a fixed point in , let a photon propagate a distance L
and then return:
Let the average speed 
.
Then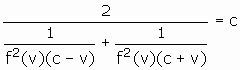 
Consequently, 
My derivation of special relativity is now complete. Because of its great similarity to Einstein’s theory, I'll write my equations with the traditional gamma:
|
|
It’s time to summarize. There are two facts that must be grasped. Relativity in the spatially compact universe SxR differs from that of ordinary SR. On the cosmological scale, SxR flaunts an absolute time order and an absolute frame of reference. Locally, the two theories are absolutely indistinguishable. Ю
Is It Possible to fall into a Black Hole?
The Schwarzschild Metric is a static spherically symmetric solution of the vacuum Einstein Field Equations. The Schwarzschild solution in standard form is:
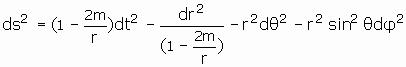
Let’s assume that the fundamental properties of a spherically symmetric gravitational field are described by this metric. I propose that we review the equations describing radial motion in this field, presupposing the postulate that an absolute time order exists. I want you to see the obvious meaning of the equations in terms of the absolute time order. I’m reasoning by analogy. Just as the equations of motion for the Schwarzschild metric are given in terms of normal time at spatial infinity, in the same way, I’d like you to envision the analogous equations of motion in terms of “cosmic time,” describing a gravitational field in a closed and bounded universe.
|
Radial motion is described by coordinates 
and 
being constant. Therefore, 
and 
. In the instance where the
coordinate r is also constant, we have
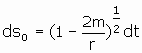
This equation expresses a comparison between an
infinitesimal amount of clock time 
for a stationary clock at r as compared to the elapsed time dt at spatial
infinity.
Consider now the proper time on a second clock as it moves in free-fall along our assigned radial line according to the equations for a geodesic. The result is
For simplicity, let’s say that if time were running
backward, then this clock moves at escape velocity (i.e., its velocity
tends toward zero as 
).
Therefore 
.
Consequently,
If we compare ds with we get
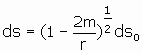
We may compare this result with the special relativity equation
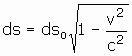
The justification for this comparison is the equivalence principle. For the instant the moving clock passes the stationary one, inertial coordinates and the Lorentz transformation apply locally. Therefore
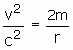
You might recall that the standard form of the Schwarzschild metric uses a system of units where c=1 and G (the gravitational constant) =1. The convention is that we can always figure out where c and G go at the last minute. If we check the units, the correct result must be
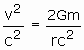
Therefore 
There is a second equation describing our geodesic,
giving us 
. Take the
Schwarzschild metric and divide by 
.
Using the result that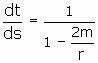 
we find that 
.
Recall that the
actual distance between two points 
and 
on
our radial line is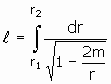 
.
Therefore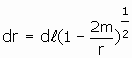 
. We have shown that .
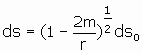Therefore 
which is what we have
already concluded.
Note: r
2m
corresponds to 
approaching the
speed of light.
Here’s the punch line to all these computations: If
you use the equations for the clock in free-fall, i.e.,
and , you can then compute the
time for the clock to fall from
to according to the absolutely
sacrosanct time at spatial infinity:
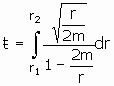
The problem is, as 2m
this integral diverges (
goes to
infinity).
A similar problem is the infinite time required for
light to reach r=2m. ds=0 for a null geodesic. Integrating dt from the Schwarzschild
metric gives us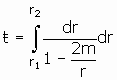 
.
The integral diverges as 2m.
By our well-ordering theorem for spacetime events, nothing can fall into a black hole until clock time at spatial infinity reads infinite time. This is impossible. The canonical, global, physically distinguished parameter that marks all events and tracks all trajectories is the time of the universe. The absolutely sacrosanct time at spatial infinity will never reach infinity. Therefore nothing can fall into a black hole.
Superluminal Velocity
An absolute frame of reference allows for motion faster than light. I propose the following generalization of Special Relativity for superluminal velocities:
The physics of this is that z=1,2,3,… is a warp factor that indexes different states of motion. One thing is incontrovertible. There is nothing about this transformation that violates the known laws of physics.
Do you have
a question or comment?
Follow it up in our Discussion
Forum.